Answer:
see explanation
Explanation:
Using the cosine addition formula
cos(A ± B ) = cosAcosB ∓ sinAsinB
Then considering the left side
cos²(45 + A) + cos²(45 - A)
= [ cos45cosA - sin45sinA ]² + [cos45cosA + sin45sinA]]²
= [
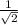 cosA -
cosA -
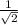 sinA ]² + [
sinA ]² + [
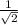 cosA +
cosA +
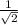 sinA ]²
sinA ]²
=
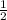 cos²A - sinAcosA +
cos²A - sinAcosA +
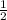 sin²A +
sin²A +
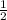 cos²A + sinAcosA +
cos²A + sinAcosA +
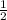 sin²A
sin²A
= cos²A + sin²A
= 1
= right side , then proven