Answer:
Step 1: -15
Step 2: b = 12, c = 36
Step 3-4: x² + 12x + 36 = -15 + 36, which simples to (x + 6)² = 21
If there is a step that has you solve for x, it should be -6 + √21 or -6 - √21.
Explanation:
Step 1 is pretty simple. All we have to do is subtract 15 from 0 to get the first blank.
x² + 12x = 0 - 15
x² + 12x = -15
Step 2:
b is the coefficient on x, which is 12.
Then, use the formula mentioned:
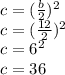
As a result of that, c is 36.
Now to substitute and simplify. (Steps 3-4)
x² + 12x + 36 = -15 + 36
To factor an equation, think about it like this: Find two numbers that add to the coefficient of x, and multiply to the constant. So what two numbers add to 12, and multiply to 36? That would be 6 & 6 (6 + 6 = 12; 6 × 6 = 36).
(x + 6)² = -15 + 36
Add 36 to -15 to get 21.
(x + 6)² = 21
That should solve steps 1-4, but I will go on ahead and give the final answer to the entire problem.
(x + 6)² = 21
Yes, you are about see what I just factored be expanded back over again. It's part of the process.
x² + 12x + 36 = 21
Now subtract 21 from both sides.
x² + 12x + 36 - 21 = 21 - 21
x² + 12x + 15 = 0
Now onto the hard part of this: the quadratic formula. a = (the understood) 1, b = 12, and c = 15.
x = (-b ± √b² - 4ac)/2a
x = -12 ± √12² - 4(15)/2
x = -12 ± √144 - 60/2
x = -12 ± ✓84/2
x = -6 + √21 or -6 - √21