Answer: True
=============================================================
Step-by-step explanation:
We'll use these two properties of integrals
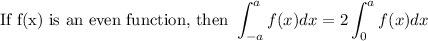
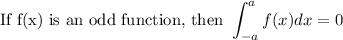
These properties are valid simply because of the function's symmetry. For even functions, we have vertical axis symmetry about x = 0; while odd functions have symmetry about the origin.
------------------------
Here's how the steps could look
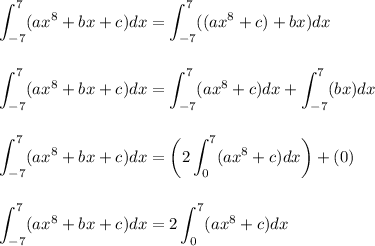
Therefore, the given statement is true. The values of a,b,c don't matter. You could replace those '7's with any real number you want and still end up with a true statement.
We can see that ax^8+c is always even, while bx is always odd.
------------------------
Side note:
For the second step, I used the idea that
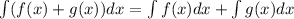
which allows us to break up a sum into smaller integrals.