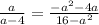Question

PLEASE HHELP!!! Bring the fraction:

b/7a^2c to a denominator of 35a^3c^3



a/a-4 to a denominator of 16-a^2

Answer 1

`(b)/(7a^2c) = (5abc^2)/(35a^3c^3)`

`(a)/(a - 4) = (-a^2 - 4a)/(16 -a^2)`

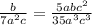
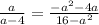
Explanation:

Given

`(b)/(7a^2c)`

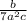
Express the denominator as
`35a^3c^3`

To do this, we divide
`35a^3c^3` by the denominator

`(35a^3c^3)/(7a^2c) = 5ac^2`

So, the required fraction is:

`(b)/(7a^2c) * (5ac^2)/(5ac^2)`

`(5abc^2)/(35a^3c^3)`

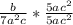
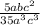
Hence:

`(b)/(7a^2c) = (5abc^2)/(35a^3c^3)`

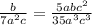
Given

`(a)/(a - 4)`

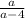
Express the denominator as
`16 - a^2`

Multiply the fraction a+4/a+4

So, we have:

`(a)/(a - 4) * ((a + 4))/((a + 4))`

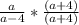
Apply difference of two squares to the denominator

`(a^2 + 4a)/(a^2 - 16)`

Take the additive inverse of the numerator and denominator

`(-(a^2 + 4a))/(-(a^2 - 16))`

`(-a^2 - 4a)/(16 -a^2)`

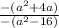
Hence:

`(a)/(a - 4) = (-a^2 - 4a)/(16 -a^2)`