Answer:
R = 40 cm
Step-by-step explanation:
From the formulae of magnification:
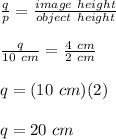
where,
q = image distance from mirror
p = object distance from mirror
Using thin lens formula:
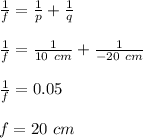
q is negative for the virtual image.
Now, the radius of the spherical mirror is double the focal length (f):
R = 2f
R = 2(20 cm)
R = 40 cm