Question

Hi, how do we do this question?​

Answer 1

`\displaystyle \int {(2x)/(3x + 1)} \, dx = (-2(ln|3x + 1| - 3x))/(9) + C`

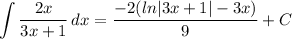
General Formulas and Concepts:

Algebra I

• Terms/Coefficients
• Factoring

Algebra II

• Polynomial Long Division

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Integration

• Integrals
• Integration Constant C
• Indefinite Integrals

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

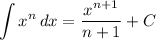
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

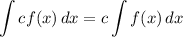
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

Logarithmic Integration

U-Substitution

Explanation:

*Note:

You could use u-solve instead of rewriting the integrand to integrate this integral.

Step 1: Define

Identify

`\displaystyle \int {(2x)/(3x + 1)} \, dx`

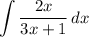
Step 2: Integrate Pt. 1

1. [Integrand] Rewrite [Polynomial Long Division (See Attachment)]:
   `\displaystyle \int {(2x)/(3x + 1)} \, dx = \int {\bigg( (2)/(3) - (2)/(3(3x + 1)) \bigg)} \, dx`
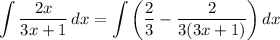
2. [Integral] Rewrite [Integration Property - Addition/Subtraction]:
   `\displaystyle \int {(2x)/(3x + 1)} \, dx = \int {(2)/(3)} \, dx - \int {(2)/(3(3x + 1))} \, dx`
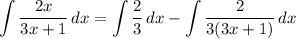
3. [Integrals] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int {(2x)/(3x + 1)} \, dx = (2)/(3)\int {} \, dx - (2)/(3)\int {(1)/(3x + 1)} \, dx`
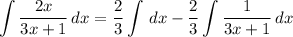
4. [1st Integral] Reverse Power Rule:
   `\displaystyle \int {(2x)/(3x + 1)} \, dx = (2)/(3)x - (2)/(3)\int {(1)/(3x + 1)} \, dx`

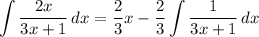
Step 3: Integrate Pt. 2

Identify variables for u-substitution.

1. Set u:
   `\displaystyle u = 3x + 1`
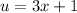
2. [u] Differentiate [Basic Power Rule]:
   `\displaystyle du = 3 \ dx`

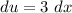
Step 4: Integrate Pt. 3

1. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int {(2x)/(3x + 1)} \, dx = (2)/(3)x - (2)/(9)\int {(3)/(3x + 1)} \, dx`
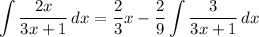
2. [Integral] U-Substitution:
   `\displaystyle \int {(2x)/(3x + 1)} \, dx = (2)/(3)x - (2)/(9)\int {(1)/(u)} \, du`
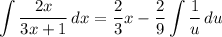
3. [Integral] Logarithmic Integration:
   `\displaystyle \int {(2x)/(3x + 1)} \, dx = (2)/(3)x - (2)/(9)ln|u| + C`
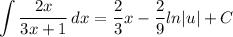
4. Back-Substitute:
   `\displaystyle \int {(2x)/(3x + 1)} \, dx = (2)/(3)x - (2)/(9)ln|3x + 1| + C`
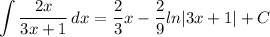
5. Factor:
   `\displaystyle \int {(2x)/(3x + 1)} \, dx = -2 \bigg( (1)/(9)ln|3x + 1| - (x)/(3) \bigg) + C`
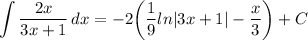
6. Rewrite:
   `\displaystyle \int {(2x)/(3x + 1)} \, dx = (-2(ln|3x + 1| - 3x))/(9) + C`

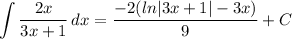
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Book: College Calculus 10e