Question

4. Consider the function g(x) = 2x^2 - 4x+3 on the interval [-1, 2]

A.) Does Rolle's Theorem apply to g(x) on the given interval? If so, find all numbers, s,
guaranteed to exist by Rolle's Theorem. If not, explain why not. (2 pts.)
b.) Does the Mean Value Theorem apply to g(x) on the given interval? If so, find all
numbers, a guaranteed to exist by the Mean Value Theorem. If not, explain why not.
(4 pts.)

Answer 1

Hi there!

A.) Begin by verifying that both endpoints have the same y-value:

g(-1) = 2(-1)² - 4(-1) + 3

Simplify:

g(-1) = 2 + 4 + 3 = 9

g(2) = 2(2)² - 4(2) + 3 = 8 - 8 + 3 = 3

Since the endpoints are not the same, Rolle's theorem does NOT apply.

B.)

Begin by ensuring that the function is continuous.

The function is a polynomial, so it satisfies the conditions of the function being BOTH continuous and differentiable on the given interval (All x-values do as well in this instance). We can proceed to find the values that satisfy the MVT:

`f'(c) = (f(a)-f(b))/(a-b)`

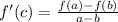
Begin by finding the average rate of change over the interval:

`(g(2) - g(-1))/(2-(-1)) = (3 - 9 )/(2-(-1)) = (-6)/(3) = -2`

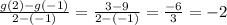
Now, Find the derivative of the function:

g(x) = 2x² - 4x + 3

Apply power rule:

g'(x) = 4x - 4

Find the x value in which the derivative equals the AROC:

4x - 4 = -2

Add 4 to both sides:

4x = 2

Divide both sides by 4:

x = 1/2