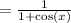Answer:
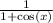
Explanation:
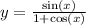
differentiating numerator wrt x :-
(sinx)' = cos x
differentiating denominator wrt x :-
(1 + cos x)' = (cosx)' = - sinx
- Let's say the denominator was "v" and the numerator was "u"
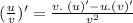
here,
- since u is the numerator u= sinx and u = cos x
- v(denominator) = 1 + cos x; v' = - sinx
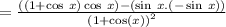
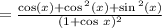
since cos²x + sin²x = 1
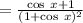
diving numerator and denominator by 1 + cos x