Answer:
The volume is increasing at a rate of 33929.3 cubic millimeters per second.
Explanation:
Volume of a sphere:
The volume of a sphere of radius r is given by:

In this question:
We have to derivate V and r implicitly in function of time, so:
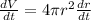
The radius of a sphere is increasing at a rate of 3 mm/s.
This means that
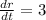
How fast is the volume increasing when the diameter is 60 mm?
Radius is half the diameter, so
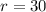 . We have to find
. We have to find
 . So
. So
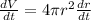

The volume is increasing at a rate of 33929.3 cubic millimeters per second.