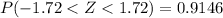Complete Question
The quality control manager at a computer manufacturing company believes that the mean life of a computer is 91 months with a standard deviation of 10 months if he is correct. what is the probability that the mean of a sample of 68 computers would differ from the population mean by less than 2.08 months? Round your answer to four decimal places. Answer How to enter your answer Tables Keypad
Answer:
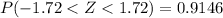
Explanation:
From the question we are told that:
Population mean \mu=91
Sample Mean \=x =2.08
Standard Deviation \sigma=10
Sample size n=68
Generally the Probability that The sample mean would differ from the population mean
P(|\=x-\mu|<2.08)
From Table
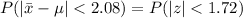
T Test
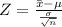

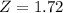
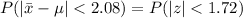
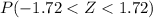
Therefore From Table