Answer:
The initial angular speed of the CD is equal to 14.73 rad/s.
Step-by-step explanation:
Given that,
Angular displacement,
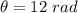
Final angular speed,
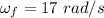
The acceleration of the CD,
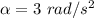
We need to find the initial angular speed of the CD. Using third equation of kinematics to find it such that,
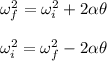
Put all the values,
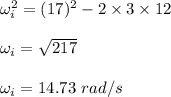
So, the initial angular speed of the CD is equal to 14.73 rad/s.