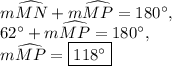Answer:
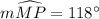
Explanation:
In any circle, the measure of an inscribed angle (an angle created when the intersection of two chords is on the circle) is equal to half of the arc it forms. In this case,
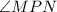 is an inscribed angle that forms
is an inscribed angle that forms
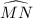 . Therefore, the measure of arc MN must be twice the measure of angle MPN:
. Therefore, the measure of arc MN must be twice the measure of angle MPN:
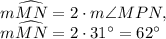
Since we want to find the measure of arc MP, we need to know that there are 360 degrees in a circle. Since
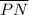 is a diameter of the circle (line that has two endpoints on the circle and that passes through the center of the circle), each side of
is a diameter of the circle (line that has two endpoints on the circle and that passes through the center of the circle), each side of
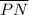 must be 180 degrees.
must be 180 degrees.
Therefore, we have: