Answer:
106 people.
Explanation:
Logistic equation:
The logistic equation is given by:
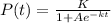
In which

K is the carrying capacity, k is the growth/decay rate, t is the time and P_0 is the initial value.
Suppose a rumor is going around a group of 191 people. Initially, only 38 members of the group have heard the rumor.
This means that
 , so:
, so:
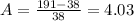
Then
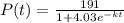
3 days later 68 people have heard it.
This means that
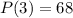 . We use this to find k.
. We use this to find k.
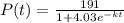
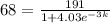
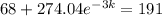
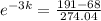
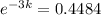
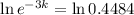
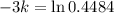


Then

How many people are expected to have heard the rumor after 6 days total have passed since it was initially spread?
This is P(6). So
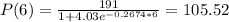
Rounding to the nearest whole number, 106 people.