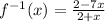Question

Find the inverse of the following function​

Answer 1

ƒ^-1 (x) =
`(2-7x)/(2+x)`

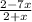
Explanation:

Substitute y for f (x)

`y = (-2x+2)/(x+7)`

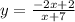
Interchange x and y

`x=(-2y+2)/(y+7)`

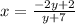
Swap the sides of the equation

`(-2y+2)/(y+7) = x`

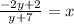
Multiply both sides of the equation by y + 7

-2y + 2 = (y + 7)x

Distribute x through the parentheses

-2y + 2 = xy + 7x

Move the expression/constant to the left-hand side and change its sign

-2y - xy + 7x - 2

Factor out from the expression

(-2 - x)y = 7x - 2

Divide both sides of the equation by -2 - x

`y = (7x-2)/(-2-x)`

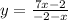
Simplify the expression

`y = (2-7x)/(2+x)`

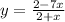
Substitute ƒ ^-1 (x) for y

`f^(-1) (x) = (2-7x)/(2+x)`

Answer 2

f-¹(x)=
`(2-7x)/(x+2)`

Answer:

Solution given:

f(x)=
`(-2x+2)/(x+7)`

Let f(x)=y

y=
`(-2x+2)/(x+7)`

Interchanging role of x and y

x=
`(-2y+2)/(y+7)`

doing crisscrossed multiplication

x(y+7)=-2y+2

now solve it:

xy+7x=-2y+2

keep like terms in one side

xy+2y=2-7x

take common

y(x+2)=2-7x

make a value of y

y=
`(2-7x)/(x+2)`

So,

f-¹(x)=
`(2-7x)/(x+2)`