Answer:
A and B
Explanation:
we would like to solve the following equation:
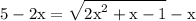
to do so isolate -x to the left hand side and change its sign:
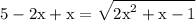
simplify addition:
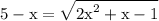
square both sides:
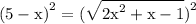
simplify square of the right hand side:
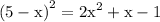
use (a-b)²=a²-2ab+b² to expand the left hand side:

swap the equation:

isolate the right hand side expression to the left hand side and change every sign:

simplify:
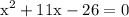
rewrite the middle term as 13x-2x:
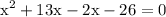
factor out x:
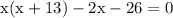
factor out -2:
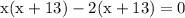
group:
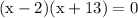
by Zero product property we obtain:

solve for x:
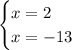
to check for extraneous solutions we can define the domain of equation recall that a square root of a function is always greater than or equal to 0 therefore
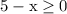
solve the inequality for x:
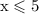
since 2 and -13 is less than 5 both solutions are valid for x hence,

and we're done!