Question

A set of quiz scores has a mean of 78 and a standard deviation of 9. Using a common grading scale where 60 and above is a passing score, what percentage of the

students passed this test?
Explain your answer in terms of the 68-95-99.7 rule.

Answer 1

97.5% of the students passed this test.

Explanation:

The Empirical Rule states that, for a normally distributed random variable:

Approximately 68% of the measures are within 1 standard deviation of the mean.

Approximately 95% of the measures are within 2 standard deviations of the mean.

Approximately 99.7% of the measures are within 3 standard deviations of the mean.

In this problem, we have that:

Mean of 78, standard deviation of 9.

What percentage of the students passed this test?

Above 60.

60 = 78 - 2*9

So 60 is two standard deviations below the mean.

The normal distribution is symmetric, which means that 50% of the measures are above the mean and 50% are below.

Of the 50% above, all passed.

Of the 50% below, 95%(within 2 standard deviations of the mean) passed.

So

`p = 0.5 + 0.5*0.95 = 0.975`

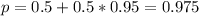
97.5% of the students passed this test.