Question

Can someone explain how to do this, I don't need a direct answer I just need an explanation.

Answer 1

• m
  `\angle`STW = 40°
• m
  `\angle` TSV = 140°

Explanation:

Here it is given that ,l ines PV , QW and RX are parallel .That is ,

`\longrightarrow PV \ || \ QW \ || RX`

And we would like to find out the value of ,

`\longrightarrow m\angle STW \ \& \ \angle TSV`

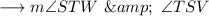
As we know that when a transversal intersects two parallel lines then ,

• Corresponding angles are equal .Also this is used as an axiom to prove that two lines are parallel .
• The sum of co- interior angles is 180° .

Here ,

`\angle STW` and
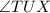`\angle TUX` are corresponding angles .So they must be equal.

`\longrightarrow x = 2y \dots (i)`

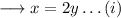
Again here
`\angle VST` and
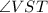`\angle STW` are co- interior angles. So ,

`\longrightarrow x + (x +5y) = 180^o \dots (ii)`

Substitute the value from equation (i) into (ii) ,

`\longrightarrow 2y + 2y +5y =180^o \\`

`\longrightarrow 9y = 180^o\\`

`\longrightarrow y =(180^o)/(9)\\`

`\longrightarrow y = 20^o`

`\rule{200}4`

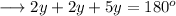
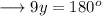
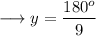
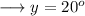
Therefore , we may find out the required angles as ,

`\longrightarrow m\angle STW = x \\`

`\longrightarrow m\angle STW = 2y\\`

`\longrightarrow m\angle STW = 2(20^o)\\`

`\longrightarrow \underline{\underline{m\angle STW = 40^o}}`

`\rule{200}4`

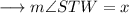
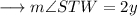
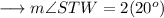
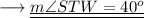
Again ,

`\longrightarrow m\angle TSV = x + 5y \\`

`\longrightarrow m\angle TSV = 40^o 5(20^o)\\`

`\longrightarrow m\angle TSV = 40^o + 100^o\\`

`\longrightarrow \underline{\underline{ m\angle TSV = 140^o }}`

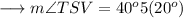
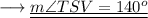
And we are done!

`\rule{200}4`