Answer:
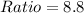
The exposure may be risk factor.
Step-by-step explanation:
Given
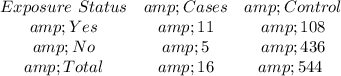
Required
The odd ratio
First, we calculate the odds of exposure using:
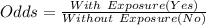
For cases, we have:
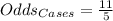
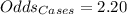
For controls, we have:
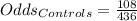
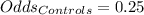
So, the odds' ratio is:
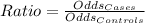
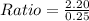
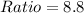
Conclusion about the odds' ratio
The calculated ratio is greater than (and also far from) 1.
This implies that there is a greater exposure than the controls.
So, we can conclude that the exposure may be risk factor.