Answer:
the required solution is; x(t) = 0.675sin( 2.222t )
Step-by-step explanation:
Given the data in the question;
Using both Newton's and Hooke's law;
m
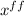 + k
+ k
 = 0,
= 0,
 (0) = 0,
(0) = 0,
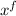 (0) = 1.5
(0) = 1.5
given that mass m = 9 kg
 = 1.8 m
= 1.8 m
k is F / x
hence
k = F / x
given that, F = 80 N
we substitute
k = 80 / 1.8
k = 44.44
so
m
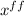 + k
+ k
 = 0,
= 0,
we input
9
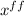 + 44.44
+ 44.44
 = 0,
= 0,
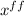 + 4.9377
+ 4.9377
 = 0
= 0
so auxiliary equation is,
r² + 4.9377 = 0
r² = -4.9377
r = √-4.9377
r = ±2.222i
hence, the solution will be;
x(t) = A×cos( 2.222t ) + B×sin( 2.222t )
⇒
 (t) = -2.222Asin( 2.222t ) + 2.222Bcos( 2.222t )
(t) = -2.222Asin( 2.222t ) + 2.222Bcos( 2.222t )
using initial conditions
x(0) = 0
⇒ 0 = A
 (t) = 1.5
(t) = 1.5
1.5 = 2.222B
so
B = 1.5 / 2.222 = 0.675
Hence, the required solution is; x(t) = 0.675sin( 2.222t )