Question

Find the limit. Use l'Hospital's Rule if appropriate. If there is a more elementary method, consider using it. lim x→[infinity] ln(5x) 5x Step 1 As x → [infinity], ln(5x) → and 5x → .

Answer 1

`\lim_(x \to \infty) (ln(5x))/(5x) = \lim_(x \to \infty) (1/x)/(5) = \lim_(x \to \infty) (1)/(5x) = 0`

Explanation:

L'Hopital's rule says that, if both numerator and denominator diverge, then we can look at the limit of the derivates.

Here we have:

`\lim_(x \to \infty) (ln(5x))/(5x)`

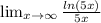
The numerator is ln(5x) and when x tends to infinity, this goes to infinity

the denominator is 5x, and when x tends to infinity, this goes to inifinity

So both numerator and denominator diverge to infinity when x tends to infinity.

Then we can use L'Hopithal's rule.

The numerator is:

f(x) = Ln(5x)

then:

f'(x) = df(x)/dx = 1/x

and the denominator is:

g(x) = 5*x

then:

g'(x) = 5

So, if we use L'Hopithal's rule we get:

`\lim_(x \to \infty) (ln(5x))/(5x) = \lim_(x \to \infty) (1/x)/(5) = \lim_(x \to \infty) (1)/(5x) = 0`