Which is the correct calculation of the y-coordinate of point A? 0 (0 - 0)2 + (1 - y2 = 2 O (0 - 1)² + (0- y2 = 22 (0-0)² + (1 - y2 = 2 (0 - 1)2 + (0-y2 = 2

Question

asked Apr 2, 2022 206k views

1 Answer

David Downes · Answer 1 · 2022-04-06T15:36:56+0000

Answer:

The y-coordinate of point A is
√(3) .

Explanation:

The equation of the circle is represented by the following expression:

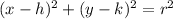(x-h)^(2)+(y-k)^(2) = r^(2) (1)

Where:

- Independent variable.

- Dependent variable.

,
- Coordinates of the center of the circle.

- Radius of the circle.

If we know that
h = 0 ,
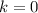k = 0 and
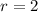r = 2 , then the equation of the circle is:

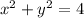x^(2) + y^(2) = 4 (1b)

Then, we clear
within (1b):

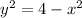
y^(2) = 4 - x^(2)

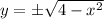$y = \pm \sqrt{4-x^(2)}$ (2)

If we know that
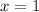x = 1 , then the y-coordinate of point A is:

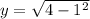
$y = \sqrt{4-1^(2)}$

y = √(3)

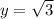
The y-coordinate of point A is
√(3) .