Question

An automobile assembly line operation has a scheduled mean completion time, , of minutes. The standard deviation of completion times is minutes. It is claimed that, under new management, the mean completion time has decreased. To test this claim, a random sample of completion times under new management was taken. The sample had a mean of minutes. Can we support, at the level of significance, the claim that the mean completion time has decreased under new management

Answer 1

The question is incomplete. The complete question is :

An automobile assembly line operation has a scheduled mean completion time, μ, of 15.5 minutes. The standard deviation of completion times is 1.7 minutes. It is claimed that, under new management, the mean completion time has decreased. To test this claim, a random sample of 90 completion times under new management was taken. The sample had a mean of 15.4 minutes. Can we support, at the 0.1 level of significance, the claim that the mean completion time has decreased under new management?

Solution :

The given data :

n = 90

μ = 15.5

σ = 1.7

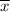`$\overline x$` = 15.4

So, the null hypothesis is :
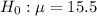`$H_0: \mu = 15.5$` is been tested against

Alternate hypothesis :
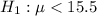`$H_1 : \mu < 15.5 $` (one-tailed test)

Since, the sample size is sufficiently large and the sample deviation is known, we use the Z-test.

Under this test, the test statistic is given as :

`$Z=(\overline x - \mu)/(\sigma/√(n)) \sim N(0,1)$`

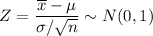
Under
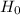`H_0`, we have

`$Z_0=(\overline x - \mu)/(\sigma/√(n)) $`

`$Z_0=(15.4-15.5)/(1.7/√(90)) $`

`$Z_0=-0.56$`

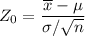
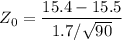
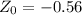
The critical value for the test is
`$Z_(\alpha) = Z_(0.1) = -1.28$`

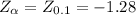
We observe that (-0.56 > -1.28), and so we fail to reject the null hypothesis.

No, there is no evidence to support the claim that the mean completion time has decreased.

Thus, we conclude that the mean completion time is 15.5 minutes.