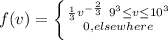Answer:
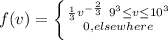
Explanation:
Given
 --- interval
--- interval
Required
The probability density of the volume of the cube
The volume of a cube is:
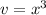
For a uniform distribution, we have:
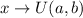
and
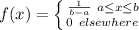
 implies that:
implies that:
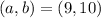
So, we have:
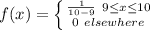
Solve
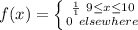
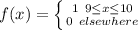
Recall that:
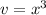
Make x the subject
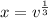
So, the cumulative density is:
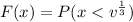
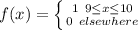 becomes
becomes
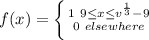
The CDF is:
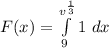
Integrate
![F(x) = [v]\limits^{v^(1)/(3)}_9](https://img.qammunity.org/2022/formulas/mathematics/college/emaxwem0udirhfiptrwftowx17yfb3owlc.png)
Expand
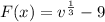
The density function of the volume F(v) is:
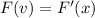
Differentiate F(x) to give:
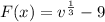
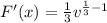
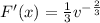
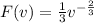
So: