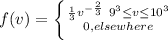Question

Suppose that the length of a side of a cube X is uniformly distributed in the interval 9

Answer 1

`f(v) = \left \{ {{(1)/(3)v^{-(2)/(3)}\ 9^3 \le v \le 10^3} \atop {0, elsewhere}} \right.`

Explanation:

Given

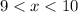`9 < x < 10` --- interval

Required

The probability density of the volume of the cube

The volume of a cube is:

`v = x^3`

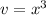
For a uniform distribution, we have:

`x \to U(a,b)`

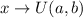
and

`f(x) = \left \{ {{(1)/(b-a)\ a \le x \le b} \atop {0\ elsewhere}} \right.`

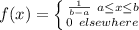
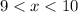`9 < x < 10` implies that:

`(a,b) = (9,10)`

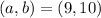
So, we have:

`f(x) = \left \{ {{(1)/(10-9)\ 9 \le x \le 10} \atop {0\ elsewhere}} \right.`

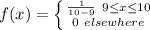
Solve

`f(x) = \left \{ {{(1)/(1)\ 9 \le x \le 10} \atop {0\ elsewhere}} \right.`

`f(x) = \left \{ {{1\ 9 \le x \le 10} \atop {0\ elsewhere}} \right.`

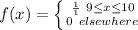
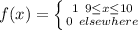
Recall that:

`v = x^3`

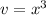
Make x the subject

`x = v^(1)/(3)`

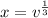
So, the cumulative density is:

`F(x) = P(x < v^(1)/(3))`

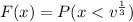
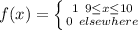`f(x) = \left \{ {{1\ 9 \le x \le 10} \atop {0\ elsewhere}} \right.` becomes

`f(x) = \left \{ {{1\ 9 \le x \le v^(1)/(3) - 9} \atop {0\ elsewhere}} \right.`

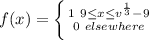
The CDF is:

`F(x) = \int\limits^{v^(1)/(3)}_9 1\ dx`

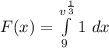
Integrate

`F(x) = [v]\limits^{v^(1)/(3)}_9`

Expand

`F(x) = v^(1)/(3) - 9`

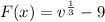
The density function of the volume F(v) is:

`F(v) = F'(x)`

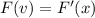
Differentiate F(x) to give:

`F(x) = v^(1)/(3) - 9`

`F'(x) = (1)/(3)v^{(1)/(3)-1}`

`F'(x) = (1)/(3)v^{-(2)/(3)}`

`F(v) = (1)/(3)v^{-(2)/(3)}`

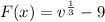
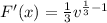
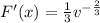
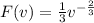
So:

`f(v) = \left \{ {{(1)/(3)v^{-(2)/(3)}\ 9^3 \le v \le 10^3} \atop {0, elsewhere}} \right.`