Answer:
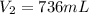
Step-by-step explanation:
Hello there!
In this case, according to the given information, it turns out possible for us to solve this problem by using the combined gas law:
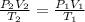
Thus, we solve for the final volume by solving for V2 as follows:
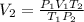
Now, we plug in the variables to obtain the result in milliliters and making sure we have both temperatures in Kelvins:

Regards!