Question

The mayor is interested in finding a 95% confidence interval for the mean number of pounds of trash per person per week that is generated in city. The study included 120 residents whose mean number of pounds of trash generated per person per week was 31.5 pounds and the standard deviation was 7.8 pounds.

Round your answers to two decimal places.

A. The sampling distribution follows a ______ distribution.

B. With 95% confidence the population mean number of pounds per person per week is between_____ and_____ pounds.

C. If many groups of 120 randomly selected people in the city are studied, then a different confidence interval would be produced from each group. About_____ percent of these confidence intervals will contain the true population mean number of pounds of trash generated per person per week and about________ percent will not contain the true population mean number of pounds of trash generated per person per week.

Answer 1

A. Normal

B. 30.1, 32.9

C. 95, 5

Explanation:

A. The sampling distribution follows a normal distribution

Given that the sample size is large, we have that the sample distribution follows a normal distribution according to the central limit theorem

B. The 95% confidence interval is given as follows;

`CI=\bar{x}\pm z * (s)/(√(n))`

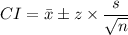
The number of residents in the study, n = 120 residents

The sample mean,
`\overline x` = 31.5 pounds

The standard deviation, s = 7.8 pounds

The z-value for 95% confidence level, z = 1.96

Therefore, we get;

C.I. = 31.5 ± 1.96 × 7.8/√(120)

The 95% C.I. ≈ 30.1 ≤
`\overline x` ≤ 32.9

Therefore, we have that with 95% confidence, the population mean number of pounds per person per week is between 30.1 and 32.9

C. Therefore, according to the central limit theorem, about 95 percent of the groups of 120 will contain the true population mean number of pounds of trash generated per person per week and about 5 percent will not contain the true population mean number of pounds of trash generated per person per week.