Question

Please help! Would be appreciated so much

Answer 1

25%.

Explanation:

First, let's find the area of both circles. The area of a circle is given by:

`\displaystyle A = \pi r^2`

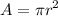
The radius of the smaller circle is one. Thus, its area is:

`\displaystyle A = \pi (1)^2 = \pi`

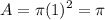
The radius of the larger circle is two. Thus, its area is:

`\displaystyle A = pi (2)^2 = 4\pi`

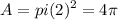
The probability that a random point chosen will be inside the small circle will be the area of the small circle over the total area. Hence:

`\displaystyle P= (\pi )/(4\pi)=(1)/(4)= 25\%`

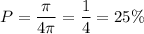
The probability of a random point being in the small circle is 25%.