Answer:
Absolute value.
Explanation:
We have the expression:
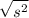
The square root and the square will cancel. This yields:
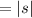
We need the absolute value because any value squared is positive. The square root of a positive value will also be positive.
In other words, if we only simplified the expression down to s without the absolute value, if s was originally negative, our simplification will have also been negative.
For instance, say s = -7, then:

However, if we let √s² = s, then s = -7. By having the absolute value, we have that |s| = |-7| = 7, which is the correct statement.