Answer:
The vertex is at (1, -108).
Explanation:
We have the function:

And we want to find its vertex point.
Note that this is in factored form. Hence, our roots/zeros are x = 7 and x = -5.
Since a parabola is symmetric along its vertex, the x-coordinate of the vertex is halfway between the two zeros. Hence:
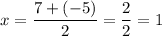
To find the y-coordinate, substitute this back into the function. Hence:
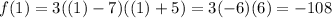
Therefore, our vertex is at (1, -108).