Answer:
The quadrilateral is a rhombus
Explanation:
Given
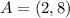

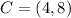
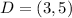
Required
The true statement
Calculate slope (m) using

Calculate distance using:
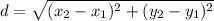
Calculate slope and distance AB

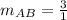
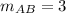 -- slope
-- slope
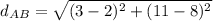
 -- distance
-- distance
Calculate slope and distance BC

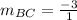
 -- slope
-- slope
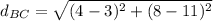
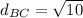 --- distance
--- distance
Calculate slope CD
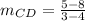
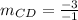
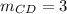 -- slope
-- slope
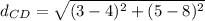
 -- distance
-- distance
Calculate slope DA
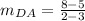
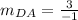
 -- slope
-- slope
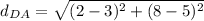
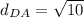
From the computations above, we can see that all 4 sides are equal, i.e.
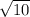
And the slope of adjacent sides are negative reciprocal, i.e.
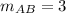 and
and

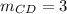 and
and

The quadrilateral is a rhombus