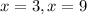Question

Log_(5)(x-4)=1-log_(5)(x-8)

Answer 1

Hello,

I suppose the question is solve for x.

`\displaystyle log_5\ (a)=(ln (a))/(ln (5)) \\\\log_5(x-4)=1-log_5(x-8)\\\\(ln(x-4))/(ln(5)) =1- (ln(x-8))/(ln(5))\\\\ln(x-4)=ln(5)-ln(x-8)\\\\ln(x-4)+ln(x+8)=ln(5)\\\\ln((x-4)*(x-8))=ln(5)\\\\(x-4)*(x-8)=5\\\\x^2-12x+27=0\\\\\Delta=12^2-4*27=36=6^2\\\\x=9\ or\ x=3\\\\Sol=\{3,9\}\\`

For Moderators,

this is a mathematical resolution without any bla-bla sentences that you will easily find. (I can not do it sorry)

Answer 2

x = 3, x = 9

Explanation:

When solving this problem, keep the general format of a logarithm in mind:

`b^x=y\\log_b(y)=x`

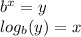
Where, (b) represents the base, (x) is the exponent, and (y) is the evalutaor. Please note that others might use slightly different terminotoly than what is used in this answer.

One is given the following expression, and is asked to solve for the parameter (x);

`log_5(x-4)=1-log_5(x-8)`

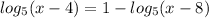
First, manipulate the exquestion such that all of the logarithmic expressions are on one side. Use inverse operations to do this.

`(log_5(x-4))+(log_5(x-8))=1`

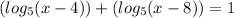
Now use the Logarithmic Base Change rule to simplify. The Logarithmic Base Change rule states the following;

`log_b(x)=(log(x))/(log(b))`

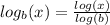
Remember, if no base is indicated in a logarithm, then the logarithm's base is (10). Apply the Logarithmic Base Change rule to this problem;

`(log(x-4))/(log(5))+(log(x-8))/(log(5))=1`

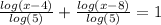
Now remove the denominator. Multiply all terms in the equation by the least common denominator; (
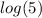`log(5)`) to remove it from the denominator on the left side.

`((log(x-4))/(log(5))+(log(x-8))/(log(5))=1)*(log(5))`

`log(x-4)+log(x-8)=log(5)`

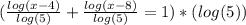
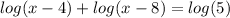
All logarithms have the same base, the left side of the equation has the addition of logarithms. This means that one can apply the Logarithm product rule. The logarithm product rules the following;

`log_b(x*y)=(log_b(x))+(log_b(y))`

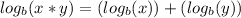
This rule can be applied in reverse to simplify the left side of the equation. Rather than rewriting the product of logarithms as two separate logarithms being added, one can rewrite it as one logarithm getting multiplied.

`log(x-4)+log(x-8)=log(5)`

`log((x-4)(x-8))=log(5)`

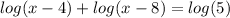
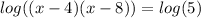
Now used inverse operations to bring all of the terms onto one side of the equation:

`log((x-4)(x-8))=log(5)`

`log((x-4)(x-8))-log(5)=0`

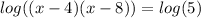
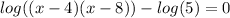
Similar to the Logarithm product rule, the Logarithm quotient rule states the following;

`log_b(x/y)=(log_b(x))-(log_b(y))`

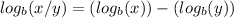
One can apply this rule in reverse here to simplify the logarithms on the left side:

`log((x-4)(x-8))-log(5)=0`

`log(((x-4)(x-8))/(5))=0`

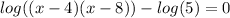
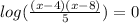
The final step in solving this equation is to use the Logarithm of (1) property. This property states the following:

`log_b(1)=0`

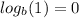
When applying this property here, one can conclude that the evaluator must be equal to (1), therefore, the following statements can be made.

`log(((x-4)(x-8))/(5))=0`

`((x-4)(x-8))/(5)=1`

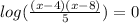
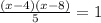
Inverse operations,

`((x-4)(x-8))/(5)=1`

`(x-4)(x-8)=5`

`(x-4)(x-8)-5=0`

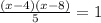
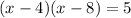
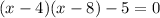
Simplify,

`(x-4)(x-8)-5=0`

`x^2-12x+32-5=0`

`x^2-12x+27=0`

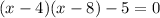
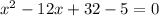
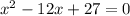
Factor, rewrite the quadratic expression as the product of two linear expressions, such that when the linear expressions are multiplied, the result is the quadratic expression:

`x^2-12x+27=0`

`(x-3)(x-9)=0`

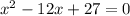
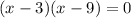
Now use the zero product property to solve. The zero product property states that any number times (0) equals (0).

`x=3,x=9`