Answer:
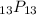
Another acceptable answer is 13! where the exclamation mark is needed.
The numeric form is 6,227,020,800 which is a little over 6 billion.
==============================================================
Step-by-step explanation:
Let's lump those four songs together to form a so called "mega song". So we treat those four items as one single item. This is ensure that those songs are played in the order we want. The other songs aren't treated this way.
We start with 16 songs and drop to 16-4 = 12 songs when taking out those four named songs. Then we add 1 to get 12+1 = 13 since we're adding in that "mega song" block.
---------------------------
So to recap so far, we've gone from 16 songs to 13 songs. The goal is to find out how many arrangements of 13 songs are possible. Order matters.
We'll use the nPr permutation function
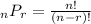
where in this case n = 13 and r = 13. Your teacher doesn't want you to evaluate this function. You simply need to state the symbolic form. So that's why we go from
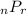 to
to
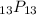
If you wanted to answer this in terms of factorial notation, then you could say this
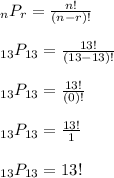
So we can see that the notations
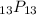 and
and
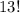 mean the exact same thing.
mean the exact same thing.
If you wanted to know the actual number of permutations, then,
13! = 13*12*11*10*9*8*7*6*5*4*3*2*1 = 6,227,020,800
which is a little over 6 billion permutations.