Question

The vertices of a triangle are P(-6,1), Q(-2,-5) and R(8,1).

Find the equation of the perpendicular bisector of the side QR

Answer 1

Explanation:

Find the slope of QR. From that we can find the the slope of the line perpendicular to QR.

Q(-2, -5) & R(8,1)

`Slope \ = (y_(2)-y_(1))/(x_(2)-x_(1))\\\\=(1-[-5])/(8-[-2])\\\\=(1+5)/(8+2)\\\\=(6)/(10)\\\\=(-3)/(5)`

So, the slope of the line perpendicular to QR = -1/m - 1÷
`(-5)/(3) = -1*(-3)/(5)=(3)/(5)`

Bisector of QR divides the line QR to two half. We have find the midpoint of QR.

Midpoint =
`((x_(1)+x_(2))/(2),(y_(1)+y_(2))/(2))`

`=((-2+8)/(2),(-5+1)/(2))\\\\=((6)/(2),(-4)/(2))\\\\=(3,-2)`

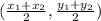
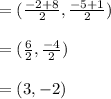
slope = 3/5 and the required line passes through (3 , -2)

y - y1 = m(x-x1)

`y - [-2] = (3)/(5)(x - 3)\\\\y + 2 = (3)/(5)x-(3)/(5)*3\\\\y=(3)/(5)x-(9)/(5)-2\\\\y=(3)/(5)x-(9)/(5)-(2*5)/(1*5)\\\\y=(3)/(5)x-(9)/(5)-(10)/(5)\\\\y=(3)/(5)x-(19)/(5)`