Answer:
The angle measures approximately 18.19°.
Explanation:
Since we want to find the angle and we are given the side adjacent to the angle and the hypotenuse, we can use the cosine ratio. Recall that:

The adjacent side is 19 and the hypotenuse is 20. Substitute:
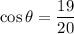
We can take the inverse cosine of both sides:
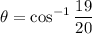
Use a calculator (make sure you're in Degrees Mode!). Hence:

The angle measures approximately 18.19°.