Answer:
1d = -3
2b = 2
2c = 1
3a = 3
3d = 4
Explanation:
Polynomial 1:
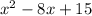
Multiply the leading coefficient, 1, and the last term, 15. You get: 15.
Then, list out the factors of 15 and the addends of -8 until you get two of numbers that are the same:
Factors of 15: -5 * -3
Addends of -8: -5 + -3
Replace the -8x with -5x - 3x:
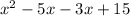
Put parentheses around the first 2 terms & last 2 terms and factor like so:


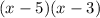
Looking at the answer (ax + b)(cx + d), d would correspond with -3.
Polynomial 2:
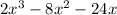
First factor out the x:
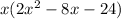
Divide the polynomial inside by 2 and place the 2 outside with the x:
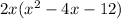
Then find the factors of 1*-12 and the addends of -4 and see which two numbers match:
Factors of -12: -6 * 2
Addends of -4: -6 + 2
Replace the -8x with -6x + 2x:
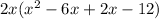
Put parentheses around the first 2 terms & last 2 terms and factor like so:
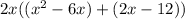

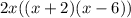
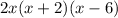
Looking at the answer (2x)(ax + b)(cx + d), b & c would correspond with 2 & 1.
Polynomial 3:
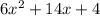
Divide the polynomial by 2:
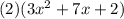
Find the factors of 3*2 and the addends of 7 and see which two numbers match:
Factors of 6: 6 * 1
Addends of 7: 6 + 1
Replace the 7x with 6x + x:
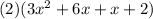
Put parentheses around the first 2 terms & last 2 terms and factor like so:
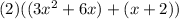
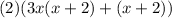
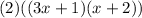
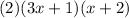
Then multiply the 2 with the (x+2) and here's your final answer:
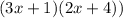
Looking at the answer (ax + b)(cx + d), a & d correspond with 3 & 4.
Hope that helps (●'◡'●)
(This took a while to write, sorry about that)