Answer:
The third number in this sequence is 63.
Explanation:
Let the first odd number be x.
Since our sequence are consecutive odd numbers, the second term must be (x + 2) and the third (x + 4). If we only add one, we will get even numbers.
Their sum is 183. Hence:
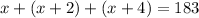
Solve for x. Combine like terms:
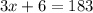
Subtract six from both sides:
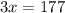
And divide both sides by three. Hence:

Therefore, our sequence is 59, 61, and 63.
The third number in this sequence is 63.
Note: If we do not get an odd number or if we get a fraction for x, we can conclude that no three consecutive integers sum to 183.