Question

Help pls!!

The functionſ is defined by f(x) = x(x + 3). If f(a) = 40 and a > 0, what is the value of a ?
A) 3
B) 5
C) 7
D) 8

Answer 1

B) 5

Explanation:

We are given the function:

`f(x)=x(x+3)`

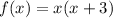
We are given that f(a) = 40 and a > 0 and we want to determine the value of a.

Substitute:

`f(a)=40=a(a+3)`

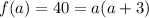
Distribute:

`a^2+3a=40`

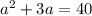
Subtract 40 from both sides:

`a^2+3a-40=0`

We can factor using 8 and -5. Hence:

`(a+8)(a-5)=0`

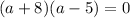
By the Zero Product Property:

`a+8=0\text{ or } a-5=0`

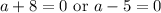
Solve for each case:

`\displaystyle a=-8\text{ or } a=5`

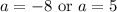
Since a > 0, we can eliminate the first solution. Hence:

`a=5`

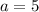
Our answer is B.