Complete question:
Given Q(x) = 7x − 3 and P(x) = 7x3 − 3x2 + 42x − 27, find P(x) ÷ Q(x) . (Divide using long division.)
Answer:
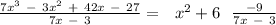
The quotient = x² + 6 and the remainder = - 9
Explanation:
Given;
Q(x) = 7x − 3
P(x) = 7x³ − 3x² + 42x − 27
To divide P(x) by Q(x) using long division, we apply the following method;
x² + 6
---------------------------------
7x − 3 √ 7x³ − 3x² + 42x − 27
− (7x³ - 3x²)
-------------------------------------
42x − 27
− (42x − 18)
----------------------------------------
− 9
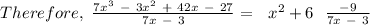
The quotient = x² + 6 and the remainder = - 9