Answer:
11 and 33
Explanation:
The the smaller number be
 . Since the other number is 3 times as large as the other, we can represent the large number as
. Since the other number is 3 times as large as the other, we can represent the large number as
 . Because they add up to 44, we have the following equation:
. Because they add up to 44, we have the following equation:
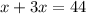
Combine like terms:
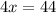
Divide both sides by 4:
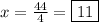
Substitute
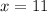 into
into
 to find the larger number:
to find the larger number:
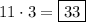
Therefore, the two numbers are 11 and 33.