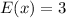Question

Javier volunteers in community events each month. He does not do more than five events in a month. He attends exactly five events 25% of the time, four events 30% of the time, three events 20% of the time, two events 15% of the time, one event 5% of the time, and no events 5% of the time. Find the probability that Javier volunteers for less than three events each month. P (x < 3) = 2 Find the expected number of events Javier volunteers in a month. 3.6 It is given that x must be below a certain value, which limits the rows to use in the PDF table. What is the sum of the probabilities of those rows?

Answer 1

`P(x < 3) = 25\%`

`E(x) = 3`

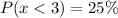
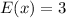
Explanation:

The given parameters can be represented as:

`\begin{array}{ccccccc}x & {5} & {4} & {3} & {2} & {1}& {0} & P(x) & {25\%} & {30\%} & {20\%} & {15\%} & {5\%} & {5\%} \ \end{array}`

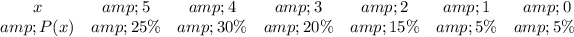
Solving (a): P(x < 3)

This is calculated as:

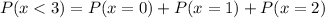`P(x < 3) = P(x = 0) + P(x = 1) + P(x =2)` ----- i.e. all probabilities less than 3

So, we have:

`P(x < 3) = 5\% + 5\% + 15\%`

`P(x < 3) = 25\%`

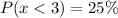
Solving (b): Expected number of events

This is calculated as:

`E(x) = \sum x * P(x)`

So, we have:

`E(x) = 5 * 25\% + 4 * 30\% + 3 * 20\% + 2 * 15\% + 1 * 5\% + 0 * 5\%`

`E(x) = 125\% + 120\% + 60\% + 30\% + 5\% + 0\%`

`E(x) = 340\%`

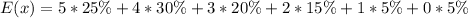
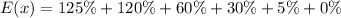
Express as decimal

`E(x) = 3.40`

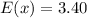
Approximate to the nearest integer

`E(x) = 3`