Answer:
B.
Explanation:

- Multiplying both numerator and denominator by (5 - 4i) , the conjugate of the denominator, i. e, (5 + 4i).
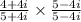
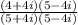
- Multiplying (4+4i) and (5-4i) using distributive property
- Using the identity (a+b)(a-b)= a² - b² where 5 will act as a and 4i will act as b
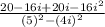
(combining like terms)
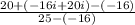
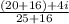
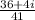
distributing the denominator
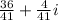
That is, option B.