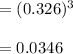Answer:
a) The probability that none of the lines experiences a surface finish problem in 41 hours of operation is 0.0498.
b)The probability that all three lines experience a surface finish problem between 24 and 41 hours of operation is 0.0346.
Explanation:
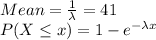
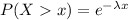
a)
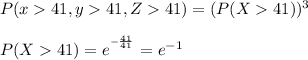
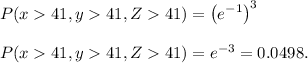
b)
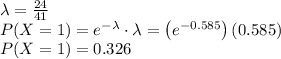
For 3 where, P(X=1, Y==1, Z=1)