Question

Candice is preparing for her final exam in Statistics. She knows she needs an 74 out of 100 to earn an A overall in the course. Her instructor provided the following information to the students. On the final, 200 students have taken it with a mean score of 68 and a standard deviation of 4. Assume the distribution of scores is bell-shaped. Calculate to see if a score of 74 is within one standard deviation of the mean.

a) Yes, 74 is the upper limit of one standard deviation from the mean.
b) Yes, the upper level of one standard deviation is 72.
c) Yes, 74 is greater than the 64, one standard deviation below the mean.
d) No, 74 is greater than the mean of 68.

Answer 1

Hence the correct option is option b) Yes, the upper level of one standard deviation is 72.

A score of 74 is not within one standard deviation of the mean.

Explanation:

Here the given details are,

Mean = 68

SD = 4

Distribution is normal.

Z-score for x = 74 is given as below:

`Z = (X - mean)/SD\\Z = (74 - 68)/4\\Z = 1.5`

So, the score of 74 is 1.5 standard deviations from the mean.

`Mean + 1*SD = 68 + 1*4 = 72Mean - 1*SD = 68 - 1*4 = 64`

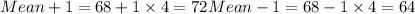
Therefore the score is not lies between 64 and 72.

Yes, the upper level of one standard deviation is 72.