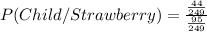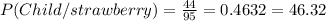Answer:
a)
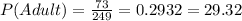
b)
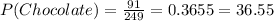
c)
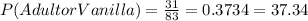
d)
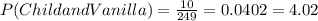
e)
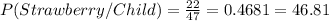
f)
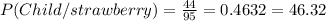
Explanation:
a)
In order to solve part a of the problem, we need to find the number of adults in the survey and divide them into the number of people in the survey by using the following formula>
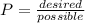
In this case we have a total of 17+43+13 adults which gives us 73 adults and a total of 249 people surveyed so we get:
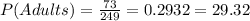
b)
The same principle works for part b
there are: 40+34+17=91 people who likes chocolate ice cream the best so the probability is:
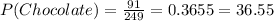
c)
when it comes to the or statement, we can use the following formula:
P(A or B) = P(A) + P(B) - P( A and B)
In this case:
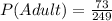
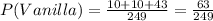
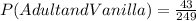
so:
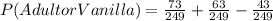
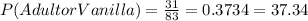
d)
Is a child and likes vanilla the best.
In the table we can see that 10 children like vanilla so the probability is:
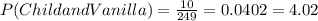
e)
Likes strawberry the best, GIVEN that the person is a child.
In this case we can make use of the following formula:
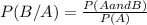
so we can get the desired probabilities. First, for the probability of the person liking strawberry the best and the person being a child, we know that 44 children like strawberry the best, so the probability is:
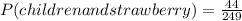
Then, we know there are 40+10+44=94 children, so the probability for the person being a child is:
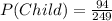
Therefore:
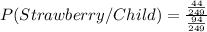
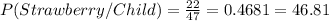
f)
The same works for the probability of the person being a child given that the person likes strawberry the best.
First, for the probability of the person liking strawberry the best and the person being a child, we know that 44 children like strawberry the best, so the probability is:
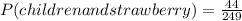
Then, we know there are 44+38+13 persons like strawberry, so the probability for the person liking strawberry is:
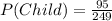
Therefore: