Question

1. Willow Brook National Bank operates a drive-up teller window that allows customers to complete bank transactions without getting out of their cars. On weekday mornings, arrivals to the drive-up teller window occur at random, with an arrival rate of 24 customers per hour or 0.4 customers per minute.

a. What is the mean or expected number of customers that will arrive in a five-minute period?
b. Assume that the Poisson probability distribution can be used to describe the arrival process. Use the arrival rate in part (a) and compute the probabilities that exactly 0, 1, 2, and 3 customers will arrive during a five-minute period.
c. Delays are expected if more than three customers arrive during any five-minute period. What is the probability that delays will occur?
2. In the Willow Brook National Bank waiting line system (see Problem 1), assume that the service times for the drive-up teller follow an exponential probability distribution with a service rate of 36 customers per hour, or 0.6 customers per minute. Use the exponential probability distribution to answer the following questions:
a. What is the probability that the service time is one minute or less?
b. What is the probability that the service time is two minutes or less?
c. What is the probability that the service time is more than two minutes?

Answer 1

1.

a. 2

b. 0.1353 probability that exactly 0 customers will arrive during a five-minute period, 0.2707 that exactly 1 customer will arrive, 0.2707 that exactly 2 customers will arrive and 0.1805 that exactly 3 customers will arrive.

c. 0.1428 = 14.28% probability that delays will occur.

2.

a. 0.4512 = 45.12% probability that the service time is one minute or less.

b. 0.6988 = 69.88% probability that the service time is two minutes or less.

c. 0.3012 = 30.12% probability that the service time is more than two minutes.

Explanation:

Poisson distribution:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following equation:

`f(x) = \mu e^(-\mu x)`

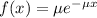
In which
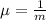`\mu = (1)/(m)` is the decay parameter.

The probability that x is lower or equal to a is given by:

`P(X \leq x) = \int\limits^a_0 {f(x)} \, dx`

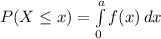
Which has the following solution:

`P(X \leq x) = 1 - e^(-\mu x)`

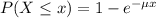
The probability of finding a value higher than x is:

`P(X > x) = 1 - P(X \leq x) = 1 - (1 - e^(-\mu x)) = e^(-\mu x)`

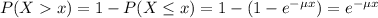
Question 1:

a. What is the mean or expected number of customers that will arrive in a five-minute period?

0.4 customers per minute, so for 5 minutes:

`\mu = 0.4*5 = 2`

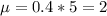
So 2 is the answer.

Question b:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-2)*2^(0))/((0)!) = 0.1353`

`P(X = 1) = (e^(-2)*2^(1))/((1)!) = 0.2707`

`P(X = 2) = (e^(-2)*2^(2))/((2)!) = 0.2707`

`P(X = 3) = (e^(-2)*2^(3))/((3)!) = 0.1805`

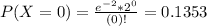
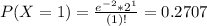
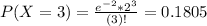
0.1353 probability that exactly 0 customers will arrive during a five-minute period, 0.2707 that exactly 1 customer will arrive, 0.2707 that exactly 2 customers will arrive and 0.1805 that exactly 3 customers will arrive.

Question c:

This is:

`P(X > 3) = 1 - P(X \leq 3)`

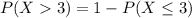
In which:

`P(X \leq 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)`

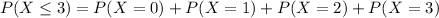
The values we have in item b, so:

`P(X \leq 3) = 0.1353 + 0.2707 + 0.2707 + 0.1805 = 0.8572`

`P(X > 3) = 1 - P(X \leq 3) = 1 - 0.8572 = 0.1428`

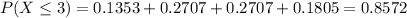
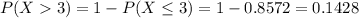
0.1428 = 14.28% probability that delays will occur.

Question 2:

`\mu = 0.6`

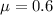
a. What is the probability that the service time is one minute or less?

`P(X \leq 1) = 1 - e^(-0.6) = 0.4512`

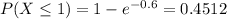
0.4512 = 45.12% probability that the service time is one minute or less.

b. What is the probability that the service time is two minutes or less?

`P(X \leq 2) = 1 - e^(-0.6(2)) = 1 - e^(-1.2) = 0.6988`

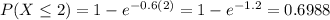
0.6988 = 69.88% probability that the service time is two minutes or less.

c. What is the probability that the service time is more than two minutes?

`P(X > 2) = e^(-1.2) = 0.3012`

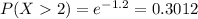
0.3012 = 30.12% probability that the service time is more than two minutes.