Question

A squirrel jumps into the air with a velocity of 4 m/s at an angel of 50 degrees. What is the maximum height reached by the squirrel?

Answer 1

Step-by-step explanation:

Assuming the squirrel is jumping off the ground, here's what we know but don't really know...

v₀ = 4.0 at 50.0°

So that's not really the velocity we are looking for. We are dealing with a max height problem, which is a y-dimension thing. Therefore, we need the squirrel's upward velocity, which is NOT 4.0 m/s. We find it in the following way:

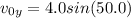`v_(0y)=4.0sin(50.0)` which gives us that the upward velocity is

v₀ = 3.1 m/s

Moving on here's what we also know:

a = -9.8 m/s/s and

v = 0

Remember that at the very top of the parabolic path, the final velocity is 0. In order to find the max height of the squirrel, we need to know how long it took him to get there. We are using 2 of our 3 one-dimensional equations in this problem. To find time:

v = v₀ + at and filling in:

0 = 3.1 - 9.8t and

-3.1 = -9.8t so

t = .32 seconds.

Now that we know how long it took him to get to the max height, we use that in our next one-dimensional equation:

Δx =
`v_0t+(1)/(2)at^2` and filling in:

Δx =
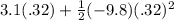`3.1(.32)+(1)/(2)(-9.8)(.32)^2` and using the rules for adding and subtracting sig fig's correctly, we can begin to simplify this:

Δx = .99 - .50 so

Δx = .49 meters