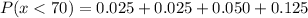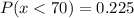Question

The accompanying data represent the homework scores for material for a random sample of students in a college algebra course.

36
47
54
58
60
66
66
68
69
70
72
75
77
77
78
78
78
79
79
79
79
79
80
82
84
85
86
86
86
87
89
89
91
92
92
93
93
94
96
99
​(a) Construct a relative frequency distribution with a lower class limit of the first class equal to 30 and a class width of 10.
(b) What is the probability a randomly selected student fails the homework​ (scores less than​ 70)? (The standard deviation is 13.64)
Simplify your answer to two decimal​ places.

Answer 1

`\begin{array}{ccc}{Class} & {Frequency} & {Relative\ Frequency} &{30-39} & {1} & {0.025} & {40-49} & {1} & {0.025} & {50 - 59} & {2} & {0.050} & {60 - 69} & {5} & {0.125} & {70 - 79} & {13} & {0.325} & {80 - 89} & {10} & {0.250} & {90 - 99} & {8} & {0.200} &{Total} & {40} & {1}\ \end{array}`

`P(x < 70) = 0.225`

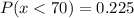
Explanation:

Given

`Lower = 30`

`Width = 10`

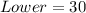
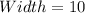
Solving (a): The relative frequency table

First, we construct the frequency table using the given parameters.

`\begin{array}{cc}{Class} & {Frequency} &{30-39} & {1} & {40-49} & {1} & {50 - 59} & {2} & {60 - 69} & {5} & {70 - 79} & {13} & {80 - 89} & {10} & {90 - 99} & {8} & {Total} & {40}\ \end{array}`

The relative frequency (RF) is calculated as:

`RF = (Frequency)/(Total)`

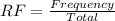
Using the above formula to calculate the relative frequency, the relative frequency table is:

`\begin{array}{ccc}{Class} & {Frequency} & {Relative\ Frequency} &{30-39} & {1} & {0.025} & {40-49} & {1} & {0.025} & {50 - 59} & {2} & {0.050} & {60 - 69} & {5} & {0.125} & {70 - 79} & {13} & {0.325} & {80 - 89} & {10} & {0.250} & {90 - 99} & {8} & {0.200} &{Total} & {40} & {1}\ \end{array}`

Solving (b):
`P(x < 70)`

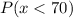
To do this, we add up the relative frequencies of classes less than 70.

i.e.

`P(x < 70) = [30 - 39] + [40 - 49] + [50 - 59] + [60 - 69]`

So, we have:

`P(x < 70) = 0.025 + 0.025 + 0.050 + 0.125`

`P(x < 70) = 0.225`