Question

An object with mass m is located halfway between an object of mass M and an object of mass 3M that are separated by a distance d. What is the magnitude of the force on the object with mass m?A) 8GMm/d^2B) GMm/(4d^2)C) 4GMm/d^2D) GMm/(2d^2)E) 3GMm/2d^2

Answer 1

A) 8GMm/d^2

Step-by-step explanation:

We are given that

`m_1=M`

`m_2=3M`

`m_3=m`

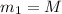
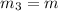
Distance between m1 and m2=d

Distance of object of mass m from m1 and m2=d/2

Gravitational force formula

`F=(Gm_1m_2)/(r^2)`

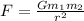
Using the formula

Force acting between m and M is given by

`F_1=(GmM)/(d^2/4)`

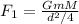
Force acting between m and 3M is given by

`F_2=(Gm(3M))/(d^2/4)`

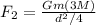
Now, net force acting on object of mass is given by

`F=F_2-F_1`

`F=(Gm(3M))/(d^2/4)-(GmM)/(d^2/4)`

`F=(12GmM)/(d^2)-(4GmM)/(d^2)`

`F=(12GmM-4GmM)/(d^2)`

`F=(8GmM)/(d^2)`

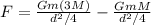
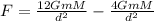
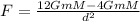
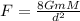
Hence, the magnitude of the force on the object with mass m=
`(8GmM)/(d^2)`

Option A is correct.