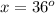Answer:
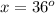
Explanation:
Given
See attachment
Required
Find x
First, calculate
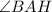
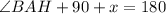 --- angle on a straight line
--- angle on a straight line
Collect like terms
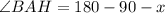
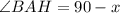
Next, calculate
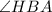
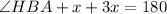 --- angle on a straight line
--- angle on a straight line
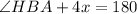
Rewrite as:
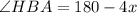
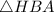 is right-angled;
is right-angled;
So:
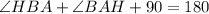
This gives:
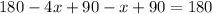
Collect like terms


Divide both sides by -5