Question

Find the third term of a geometric progression if the sum of the first three terms is equal to 12, and the sum of the first six terms is equal to (−84).

Answer 1

Given:

The sum of the first three terms = 12

The sum of the first six terms = (−84).

To find:

The third term of a geometric progression.

Solution:

The sum of first n term of a geometric progression is:

`S_n=(a(r^n-1))/(r-1)`

Where, a is the first term and r is the common ratio.

The sum of the first three terms is equal to 12, and the sum of the first six terms is equal to (−84).

`(a(r^3-1))/(r-1)=12` ...(i)

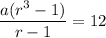`(a(r^6-1))/(r-1)=-84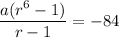` ...(ii)

Divide (ii) by (i), we get

`(r^6-1)/(r^3-1)=(-84)/(12)`

`((r^3-1)(r^3+1))/(r^3-1)=-7`

`r^3+1=-7`

`r^3=-7-1`

`r^3=-8`

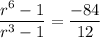
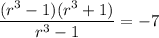
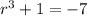
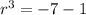
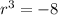
Taking cube root on both sides, we get

`r=-2`

Putting
`r=-2` in (i), we get

`(a((-2)^3-1))/((-2)-1)=12`

`(a(-8-1))/(-3)=12`

`(-9a)/(-3)=12`

`3a=12`

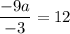
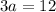
Divide both sides by 3.

`a=4`

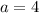
The nth term of a geometric progression is:

`a_n=ar^(n-1)`

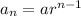
Where, a is the first term and r is the common ratio.

Putting
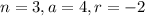`n=3,a=4,r=-2` in the above formula, we get

`a_3=4(-2)^(3-1)`

`a_3=4(-2)^(2)`

`a_3=4(4)`

`a_3=16`

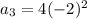
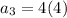
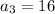
Therefore, the third term of the geometric progression is 16.